As Contribuições Astronômicas de Galileu Galilei Para a Teoria Heliocêntrica

            A primeira grande contribuição à teoria heliocêntrica foi dada por Galileu[13], com a descoberta dos satélites de Júpiter, pois pelo menos alguma coisa não girava ao redor da Terra, como afirmavam os Ptolomaicos. Derrubou, assim, o dogma de que somente um sistema estacionário (Terra) poderia ser o centro do Universo.

            Outra grande contribuição de Galileu foi a descoberta das fases de Vênus, mostrando que as variações de brilho eram devido a uma órbita ao redor do Sol.

            Galileu foi fervoroso defensor de heliocentrismo de Copérnico. Foi seu principal divulgador, tanto que caiu nas garras da Inquisição e só não foi queimado porque renegou tudo que disse e era muito bajulador.

            Inúmeros livros de divulgação científica dizem que, apesar de Galileu não ter sido o inventor da luneta, tem o mérito de ter sido o primeiro a apontá-la para o céu. Isso, porém, é uma informação equivocada. O primeiro homem a apontar uma luneta para os céus foi um inglês chamado Thomas Harriot [1560 – 1621], o primeiro cartógrafo da Lua, contemporâneo de Galileu.

O Modelo Final do Sistema Solar por Johannes Kepler

            Kepler[14] tinha inicialmente a ambição de ser pastor luterano, mas na Universidade de Tubingen, sob a influência de um professor de matemática e astronomia, abandonou a teologia e estudou astronomia. Este professor ensinou que Ptolomeu estava certo, mas Kepler preferiu o modelo de Copérnico.

            Kepler publica Mysterium Cosmographicum. Manda cópias para Brahe e Galileu. Brahe o convida para ser seu assistente em 1600, em Praga, um ano antes da morte de Brahe.

            A reunião de Brahe e Kepler é de grande importância para a astronomia. Brahe era ótimo observador, mas não tão bom teórico, enquanto Kepler era ótimo teórico e muito persistente em seus propósitos. Quando Brahe morreu, em 1601, seus dados observacionais - que eram muitos - ficaram à disposição de Kepler. Com estes dados, Kepler descobriu as Leis do Movimento Planetário.

            Depois de mais de cinco anos de trabalho tedioso com os dados observacionais de Ticho, das posições de Marte, Kepler concluiu que a órbita de Marte era uma elipse, com o Sol num foco.

            Em 1609, Kepler publicou suas duas primeiras Leis:

            Com a primeira Lei, extremamente simples, substituiu todos os ciclos e epiciclos dos modelos ptolomaico, copernicano, tichônico, etc.(Fig. 46)

Fig. 46- Lei das órbitas. A órbita de um planeta é uma elipse, com o Sol num dos focos[15].

Fig. 47- Lei das áreas. O raio vetor do planeta varre áreas iguais em iguais intervalos de tempo.

            Com a segunda, ele mostrou que os corpos não têm velocidades (em módulo) constantes, mais sim velocidades maiores quando próximos do Sol e velocidades menores quando mais afastados do Sol.

            Através destas Leis, Kepler tira de vez a Terra do centro do Universo e tira também o Sol do centro do Universo. Não se fala mais em centro do Universo e a Terra tem que girar sobre si mesma.

            Mesmo depois de publicadas estas Leis (1609), Galileu foi condenado (1633). Não havia evidência para a rotação da Terra e a Bíblia possui passagens que dizem que a Terra não gira, etc.

            Dez anos mais tarde, Kepler publica sua terceira Lei (1619), num livro cheio de misticismo, do qual só se aproveita mesmo, sua terceira Lei.

            Kepler conhecia os períodos e distâncias dos planetas. Em termos do período da Terra (=1 ano) e da distância da Terra ao Sol (º1 unidade) os períodos dos planetas e suas distâncias ao Sol são:

            Exercício 1: Calcule para cada planeta, a razão:  Confira:

Conclusão: T²/D³ 1

            Exercício 2: Sabendo-se que a distância dos planetas Urano, Netuno e Plutão ao Sol (em termos da distância Terra-Sol) são: Urano (D_U) 19,19 ; Netuno (D_N) 30,08 e Plutão (D_P) 39,46, calcule seus períodos (em unidades de anos terrestres).[16]

            Kepler disse que as trajetórias dos planetas são  elipses, com o Sol num focos, mas qual é a forma da órbita (elipse) da Terra? Qual é o achatamento dessa elipse? Antes, porém, vejamos a definição de excentricidade (e) - medida do achatamento - de um elipse (Fig.48).

Fig. 48- a = semi-eixo maior; b = semi-eixo menor; c = distância focal; e = excentricidade

            e = ; a ² = b² + c²; b =  . Assim, se c = 0  Þ e = 0 \ b = a ou seja, temos um círculo.

            Se c = a Þ  e = 1 e \ b = 0, ou seja, temos uma linha (elipse de máximo achatamento), logo 0 £ e £ 1

Exercício 3: Dados os valores da excentricidade (e) e do semi-eixo maior (a) dos planetas, calcular para cada planeta:

a) a distância ( c ) de afastamento do Sol em relação ao centro da elipse;

b) a distância ( b );

c) a diferença (a - b);

d) a distância do periélio (a - c) ( distância de menor afastamento do planeta em relação ao Sol);

e) a distância do afélio (a + c) ( distância de máximo afastamento do planeta em relação ao Sol).

Dados:

a) e = c / a Þ  c = e × a

b) b =

c) a - b

d) a - c

e) a + c

a º semi-eixo maior

b º semi-eixo menor

c º a - b

a - c = periélio (menor distância do planeta ao Sol)

a + c = afélio (maior distância do planeta ao Sol)

e = excentricidade

Veja os resultados na tabela abaixo:

( P = Planeta; M = Mercúrio; V = Vênus; T = Terra; M = Marte; J = Júpiter; S = Saturno; U = Urano; N = Netuno; P = Plutão.)

Newton e a Lei da Gravitação Universal

            Isaac Newton[17] nasceu em 1642 (um ano depois da morte de Galileu), no dia de Natal. Filho póstumo de um fazendeiro, teve de custear seus estudos trabalhando e foi graças a ajuda de um tio que conseguiu entrar em Cambridge, em 1661. Quando se bacharelou, em 1665, Isaac Barrow[18], seu professor de matemática, encorajou-o a permanecer em Cambridge.

            Naquela época, Londres era uma cidade muito poluída e com péssimo saneamento. Num livro onde se propunha um plano para reduzir a poluição atmosférica produzida pelas fábricas, “Fulmifugium”, de John Evelyn, publicado em 1661, lê-se: “O viajante fatigado, a muitas milhas de distância, reconhece a cidade pelo olfato antes que pela vista. No verão de 1665, a peste se alastrou rapidamente por Londres, dizimando cerca de 70.000 pessoas, a sétima parte da população. Um ano mais tarde sobreveio o Grande Incêndio de Londres, que arrasou dois terços da cidade.

            A peste provocou o fechamento da Universidade e Newton refugiou-se em sua fazenda de Woolsthorpe. A melhor descrição do que ele fez nesse período foi dada por ele próprio, 50 anos depois.

            “No princípio de 1665, achei o método para aproximar séries e a regra para reduzir qualquer potência de um binômio a uma tal série” (binômio de Newton e série binomial). “No mesmo ano, em maio, achei o método das tangentes de Gregory e Slusius” (fórmula de interpolação de Newton) “e em novembro o método direto das fluxões” (Cálculo diferencial); “no ano seguinte, em janeiro, a teoria das cores” (experiências com o prisma sobre decomposição da luz branca), “e em maio os princípios do método inverso das fluxões” (cálculo integral), “e no mesmo ano (1666) comecei a pensar na gravidade como se estendendo até a órbita da Lua, e da Lei de Kepler sobre os períodos dos planetas deduzi que as forças que mantêm os planetas em suas órbitas devem variar inversamente com os quadrados de suas distâncias aos centros em torno dos quais os descrevem: tendo então comparado a força necessária para manter a Lua em sua órbita com a força da gravidade na superfície da Terra e encontrado que concordam bastante bem. Tudo isso foi nos dois anos da peste, 1665 e 1666, pois naqueles dias eu estava na flor da idade (23-24 anos) para invenções, e me ocupava mais da matemática e filosofia (“física”) do que em qualquer época posterior.”

A Lei da Gravitação Universal Para Órbitas Circulares

            Já vimos que a excentricidade dos planetas é próxima de zero, o que faz as órbitas serem aproximadamente circulares, cujo movimento é muito mais simples de se estudar.

            Para uma órbita circular, a 2ª Lei de Kepler (Lei das Áreas) implica que o movimento seja uniforme.

            Todo e qualquer corpo que descreva um movimento circular e uniforme (MCU) está sob a ação de uma força centrípeta (ou radial ou central) que tem a seguinte forma:

F =  (1)

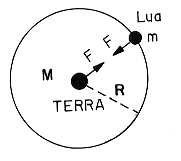
Fig. 49

Observação: o termo é propriedade do MCU e, portanto, válida qualquer que seja a origem da força F. Mas, V é a velocidade do corpo sobre o círculo, a qual é obtida sabendo-se o período (T) do movimento e o raio, assim:

V =   (2)

Substituindo esta expressão na anterior, obtemos:

F = × =  ×  =  (3)

Mas, pela 3ª Lei de Kepler, obtivemos que:

 = K \ = T = KR³ (4)

Substituindo o T² na expressão anterior, obtemos:

F = \ F =  (5)

Conclusões:

            Pela propriedade do MCU e pela 3ª Lei de Kepler, Newton concluiu que a força entre os corpos celestes cai com o quadrado da separação entre eles e é proporcional ao produto de suas massas, pois, pela 3ª Lei de Newton (ação e reação) força da Lua sobre a Terra (no exemplo estudado) é igual à força desta sobre aquela, assim, Newton foi levado à expressão:

F­_g = G  - Lei de Newton de gravitação ( 6 )

onde rescrevemos as constantes anteriores (4/K) como sendo G, que seria então uma “constante universal’, característica da força gravitacional.

            Uma vez inferida a forma da lei, vejamos o que Newton fez para testá-la.

A Lua e a Maçã

            Em sua “Philisophie de Newton” (1738) o filósofo francês Voltaire[19] conta: “Um dia no ano de 1666, Newton, então em sua fazenda, vendo uma fruta cair de uma árvore, segundo me disse sua sobrinha, Mme. Conduit, começou a meditar profundamente sobre a causa que atrai todos os corpos na direção do centro da Terra”.

            A história provavelmente é apócrifa, mas o próprio Newton confirma no trecho anteriormente citado, que comparou naquele ano “a força necessária para manter a Lua em sua órbita com a força de gravidade na superfície da Terra.”

Vamos fazer essa comparação entre a Lua e a maçã:

A força da Terra sobre a Lua é:

F_TL =  (7)

onde M_L = massa da Lua, M_T = massa da Terra R­_TL = Distância Terra-Lua.

            Newton, inicialmente, não conhecia o valor da constante G, logo, o teste que ele fez não deveria depender de G, isso é conseguido através de razões entre forças.

            Fazendo uso da equação ( 3 ), podemos rescrever o lado esquerdo da equação ( 7 ):

 (8)

onde T_L é o período da Lua ao redor da Terra.

A força da Terra sobre uma maçã é :

F_Tm =  (9)

a qual é igual à força peso (mg) que conhecemos; logo, podemos rescrever a equação (9 ) assim :

m_m × g =       (10)

sendo que g = 9,8 m/s² é a aceleração gravitacional local .

            Newton queria testar a dependência com R² no denominador de sua lei e não conhecia G nem a massa da Terra, então ele dividiu a equação ( 10 ) pela ( 8 ):

 =  =

R_TL = 385.000 km = 385.000.000 m; R_T = 6.400 km = 6.400.000 m; T_L = 27,3 dias = 27,3 x 24 x 60 x 60 seg  = 2.358.720 seg; g =  9,8 m/s²

            Newton conhecia estes valores e se sua fórmula estivesse certa, a equação acima seria verdadeira.

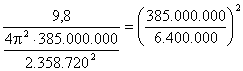
3587  3816

            Newton considerou que estes números concordavam bastante bem.

            Newton realizou assim uma das mais notáveis sínteses da história da ciência, relacionando a queda dos corpos na superfície da Terra com a órbita da Lua.

            Pode-se provar que a partir da Lei de Newton da Gravitação, pode-se reproduzir as três leis de Kleper.

            Resta um problema ainda: como determinar o valor da constante G ?

Determinação do Valor de G

            Para determinar o valor de G (constante gravitacional), é preciso medir a força de atração gravitacional entre duas massas conhecidas, o que é muito difícil no laboratório por ser muito fraca a interação gravitacional. A primeira medida foi feita por Cavendish[20] em 1798, utilizando um aparelho extremamente sensível, a balança de torção

(Fig. 12).

Sendo F = , G =

Fig. 50- Esquema de balança de torção.

            Um par de esferas da massa m nas extremidades de uma barra é suspenso pelo centro da barra por uma fibra fina de quartzo numa posição de equilíbrio AB da figura. Trazem-se então duas outras esferas de massas M à mesma distância das esferas de massa m, o que produz uma rotação devido às forças gravitacionais entre cada par de esferas. Essa rotação é muito pequena, mas pode ser observada com auxílio do espelho. Conhecendo-se a constante de torção da fibra, sabe-se a força que agiu sobre ela. As massas M , m e r são medidas facilmente, assim, Cavendish obteve para G o valor 6,71 x 10 ^-11  Nm² / kg².

            Experiências mais sofisticadas dão o valor de G atualmente aceito:

G = 6,67 × 10^-11  Nm² / kg²

“Pesando” o Sol

                        Sabemos que a força gravitacional entre o Sol e a Terra é:  mas F causa, aproximadamente, movimento circular e uniforme (MCU), logo

F =  e 

Substituindo V_T em F, obtemos:

\   

(Observe que acabamos de encontrar a Terceira Lei de Kepler ).

            Queremos a massa do Sol:

\       (11)

OBS: Esta fórmula vale também para planeta, desde que ele tenha um satélite com período (T) e distância satélite-planeta (D) conhecida. Utilizando D_TS e T da Terra  ao redor do Sol:

D_TS @ 149.000.000 km  =  149.000.000.000  m  é a distância Terra-Sol e

T = 1 ano é o período da Terra ao redor do Sol:

T  =  1 ano  =  1 × 365,24 × 24 × 60 × 60 = 31.556.736 seg (transformamos o ano em segundos)

Substituindo esses valores na última fórmula:

M_S =

M_S @ 1.960.000.000.000.000.000.000.000.000.000 kg ou M_S @ 1,96 × 10³⁰ kg

            O diâmetro (D_S) do Sol pode ser medido; assim sendo, podemos medir a densidade do Sol pela fórmula:

sendo o diâmetro do Sol D_S = 1.390.000.000 m = 1,39 × 10⁹ m

Atenção: Com a mesma fórmula (11) M =  ×  podemos determinar a massa de qualquer planeta, basta que ele tenha um satélite e seja conhecido seu período e raio médio da órbita deste satélite.

“Pesando” a Terra

            Sendo peso = força gravitacional ®  . Assim,  ou

M =  (12)

G = 6,67 x  10 ^-11  N m² / kg² (valor determinado por Cavendish)                                         (13)

R = 6.378 km =  6.378.000 M                                                                                              (14)

(Raio da Terra - Valor determinado por Eratóstenes ~ 234 a.C )

Método Para Determinar o Raio da Terra ( R_T)

Eratóstenes[21] sabia que em Siene (S), num certo dia do ano, o Sol ficava a pino (no zênite) e que no mesmo dia, em Alexandria (A), (a oitocentos mil metros de Siene) o Sol ficava a 7º (sete graus do zênite) (Fig. 14); logo, temos a seguinte regra de 3:

comprimento do círculo:           2 R  _______  360º

800.000 m ______ 7º

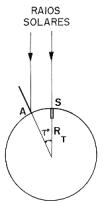
Fig. 51

\  = 800.000 × 360º \ R =  = 6.548.000 m ou R_T = 6.548 km[22].

            Falta determinar o g ( a aceleração gravitacional local). Podemos determinar g através do movimento pendular :onde T = período de oscilação do Pêndulo e L = comprimento do pêndulo \ g =  4

            Fazendo a experiência encontraremos um valor próximo de:

g = 9,8 m/s²       (15 )

            Substituindo os valores (13), (14) e (15) na equação (12) encontramos a massa da Terra:

M_T = = 5,98 × 10²⁴ kg

Exercício 4: Determinar a Densidade da Terra

“Pesando” Marte (e/ou qualquer planeta que tenha pelo menos um satélite natural ou artificial).

Usar equação (11): , onde M_P é a massa do planeta, R é distância média do planeta ao seu satélite e T é o período deste satélite ao redor do seu planeta. Use a tabela dada. Dela obtenha o período orbital ( T ) do satélite Fobos e sua distância ao planeta Marte:

Da tabela:

T = 7,70 h = 7,70 × 60 × 60 seg = 27.720 seg

R = 9,4 × 10 ³ km  = 9,4 × 10³ × 10³ m = 9,4 x 10⁶ m

M_Marte = .

Assim, a massa de Marte é 6,39 × 10²³ kg.

Exercício 5: Qual a densidade de Marte ? (Veja tabela para obter o diâmetro.) Use a equação (12) para calcular o g (aceleração gravitacional) da superfície de Marte:

(12) ® g­_M =

g_M =

Exercício 6: Qual o seu peso (p = mg) em Marte? (lembre-se: massa é constante.)

M_prof = 82 kg

P = 82 × 3,69 = 302,6 N (N = Newton)

Na Terra o peso deste professor é: P_Terra = 82 × 9,8 = 803,6 N logo, no planeta Marte serei mais leve.

Exercício 7: Determine a massa, a densidade e a aceleração gravitacional (g) para todos os planetas do Sistema Solar. (Use tabela dada.)

Exercício 8: Calcule a constante da 3ª Lei de Kepler (T² / D³ = K) para os satélites de Júpiter e Saturno. (Use a tabela dada.)

Exercício 9: Calcule a velocidade de um ponto da superfície da Terra (próximo do Equador) devido à rotação da própria Terra:

V =  (comprimento do círculo equatorial)

V =  1670 km/h  ! ! !

Exercício 8: Calcule a velocidade da Terra ao redor do Sol:

V =

V =  107.159   km/h ! ! !