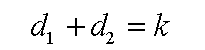
| Voltar |
PRIMEIRA LEI DE KEPLER - LEI DAS ÓRBITAS
Instituto de Física UERJ
Nesta atividade vamos desenhar as órbitas dos planetas e de alguns cometas, usando as excentricidades conhecidas das respectivas órbitas. Observaremos que as órbitas dos cometas periódicos são, em geral, muito excêntricas enquanto a dos planetas são pouco excêntricas. Objetivamos também, mostrar que, aqueles que conhecem esta lei, fazem uma idéia completamente errada da excentricidade das órbitas dos planetas, pois as consideram muito mais excêntricas do que realmente o são, isto devido, principalmente, aos desenhos destas órbitas que se vê nos livros didáticos.
O enunciado da primeira lei de Kepler, ou lei das órbitas, diz que:
Todo planeta descreve uma órbita elíptica ao redor do Sol, estando este num dos focos da elipse.
Define-se uma elipse como o conjunto dos pontos cuja soma das distâncias (d1 e d2) destes pontos a dois pontos fixos (F1 e F2), chamados focos, é uma constante (k), isto é:
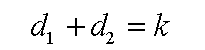
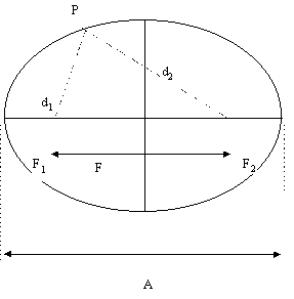
Figura 33
Definimos a excentricidade (achatamento) da elipse como sendo a razão entre a distância entre os focos (F = F1 F2) ( ou distância interfocal) e o comprimento do eixo maior (A). Representamos a excentricidade da elipse pela letra e, assim sendo:

Um círculo é um caso particular de uma elipse, isto é, o círculo é uma elipse sem achatamento algum, ou como chamamos, de excentricidade nula, pois os focos são coincidentes com o centro do círculo e assim sendo, F = 0, e, portanto, e = 0
Excentricidade das órbitas dos planetas
|
Planeta |
Excentricidade |
|
Mercúrio |
0,2 |
|
Vênus |
0,007 |
|
Terra |
0,02 |
|
Marte |
0,09 |
|
Júpiter |
0,05 |
|
Saturno |
0,06 |
|
Urano |
0,05 |
|
Netuno |
0,009 |
|
Plutão |
0,25 |
Para desenharmos as órbitas precisamos executar dois passos:
1. Descobrir qual é a distância entre os focos. Mas conhecida a excentricidade e e escolhido o comprimento do eixo maior A, arbitrariamente, como sendo, por exemplo 20 cm, obtemos a distância interfocal F, pelo produto:
![]()
Por exemplo, para a excentricidade de Mercúrio (e = 0,2) e A = 20 cm, temos que
F = 0,2 x 20 = 4,0 cm
2. Descobrir qual é o comprimento L do barbante a ser usado para desenhar a elipse. Vamos usar o método do jardineiro. Esse comprimento é dado pela soma de F mais A, ou seja:
![]()
Em nosso exemplo, A = 20 cm e F = 4,0 cm, logo L = 24 cm, assim sendo, é só cortar um pedaço de barbante com pouco mais de 24 cm, por exemplo, 28 cm, para que possamos amarrar as pontos (CD) do barbante, que definem o comprimento L = 24 cm, como mostra a figura abaixo:
barbante
![]()

Figura 34
Em seguida é só abrir um compasso com a separação F (ou fincar dois pregos separados pela distância F), envolver as pontas do compasso com o barbante do item 2 acima e, com um lápis sempre na vertical, e o barbante sempre esticado, traçar a elipse, como ilustra a figura abaixo.
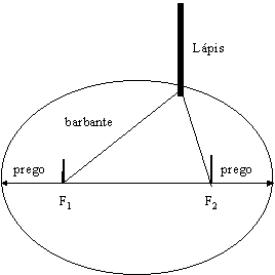
Fig 35. Esquema do método do jardineiro para desenhar uma elipse
Exemplo de elipses com 10 diferentes excentricidades:
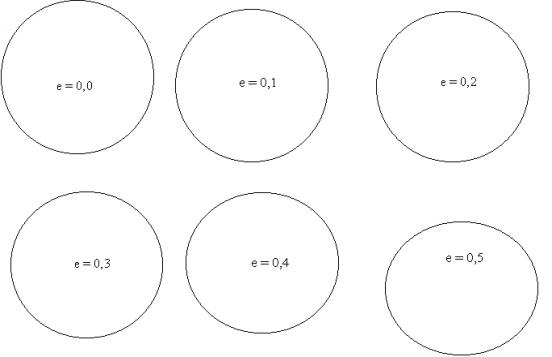


Figura 36
Conhecendo-se a definição de excentricidade, conhecendo-se as excentricidades das órbitas dos planetas e desenhando-se as mesma vemos que estas órbitas são muito aproximadamente circulares, ao contrário do que comumente se pensa. A órbita dos cometas, por outro lado, são muito mais excêntricas que as dos planetas e se assemelham mais à figura referente a e = 0,9. A órbita de Plutão, o planeta cuja órbita tem a maior excentricidade entre todos os planetas dos sistema solar está desenhada, em escala, na página seguinte. A posição do Sol na figura 36a. está no local correto também.
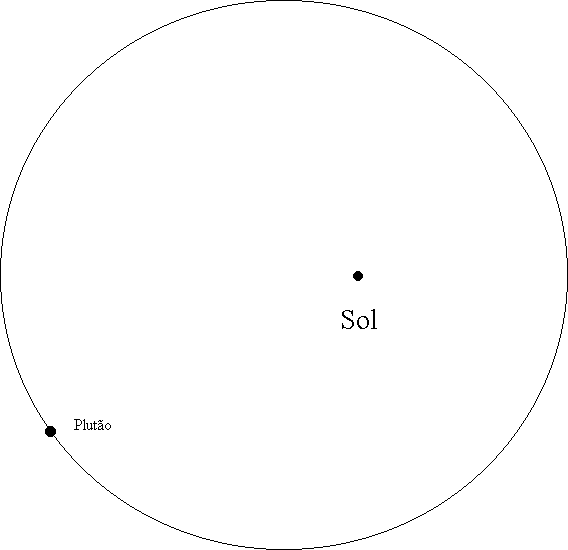 |
Fig. 36a.Órbita de Plutão. Excentricidade: 0,25
| Sobe |